Propulsione Inerziale

Pagina quasi completa

Per comprendere come sia possibile ottenere una propulsione, che può spostare nello spazio un corpo qualsiasi, diversa da quelle comunemente conosciute, come ad esempio la propulsione ad elica, turbina, o quella che sfrutta i propellenti per lanciare nello spazio razzi o simili, bisogna conoscere due concetti della meccanica.

Il primo riguarda l’inerzia di un corpo, il secondo riguarda la composizione delle forze.

La propulsione inerziale, sfrutta il primo principio della dinamica o principio d’inerzia

Un corpo persevera nel suo stato di quiete o di moto rettilineo uniforme, finchè non interviene una forza esterna interviene a modificare tale stato.

Per comprendere meglio cosa significa, potete guardare il sito cetris che spiega egregiamente, con semplici animazioni, quali sono gli effetti dell’inerzia su un corpo.

La tendenza di ogni corpo a mantenere lo stato quiete o di moto, si definisce Inerzia .

Composizione delle forze

L’idea originale era di un trattato completo che spiegasse cosa sono le forze e le conseguenze della loro applicazione ad un punto, ma penso sia più facile spiegare brevemente come si compongono tra di loro due forze e come calcolare la “Risultante”.

La risultante è quella forza, “Unica” che produce sul corpo, lo stesso effetto, di tutte le forse che su di esso sono applicate.

E’ facile comprendere come la risultante di due forze che hanno lo stesso piano e si trovano sullo stesso asse, sia la somma o la differenza tra le forse stesse a seconda che siano nello stesso verso o di verso contrario.

L’esempio classico di forse diverse di senso opposto è quelo del tiro alla fune.

Se le due forze F1, F2 hanno direzioni qualsiasi, la loro risultante R è data dalla diagonale del parallelogramma delle forze (fig.3), oppure dal lato di chiusura del triangolo delle forze (fig. 4).

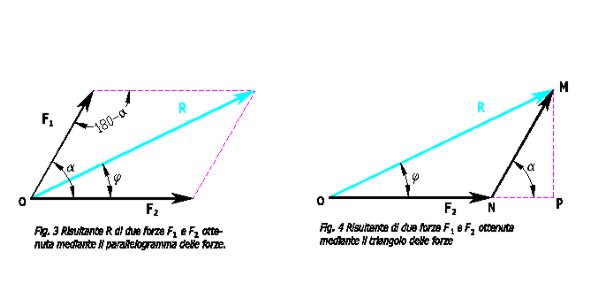
Analiticamente, applicando il teorema di Carnot al triangolo OMN ed usando indicati nella figura 4, si ha:

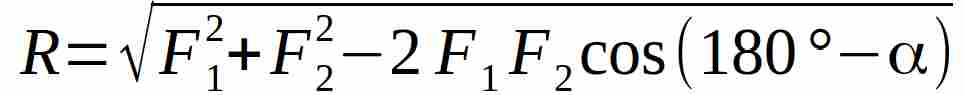
Ed essendo: cos(180° – a) = – cos a, si ottiene per la Risultante la formula:

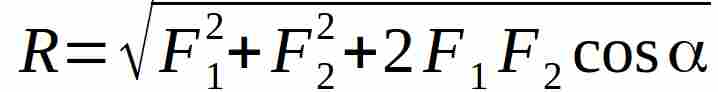
Naturalmente non c’è limite al numero di forze che possono agire su uno stesso punto, così per passi sucessivi si può calcolare la risultante

di un sistema di numero, composto di svariate forze.

Il sistema che ho ideato io si compone di un gruppo composto da 16 masse che genereranno di conseguenza, 16 Forze Centrifughe.

Provate ora a pensare ad uno di quei compattatori vibranti che si usano per assetare il materiale dopo lo scavo.

Se li avete osservati bene, vedrete che c’è un momento che si sollevano da terra e poi ricadendo, compattano il materiale.

Quei compattatori “vibrano”, ma è il principio della propulsione inerziale.

La vibrazione è data da un almero che ruota sul quale è fissata una massa eccentrica e quindi la forza centrifuga che genera è variabile e rotante.

Il mio meccanismo invece “convoglia” in una sola direzione la risultane di tutte le forze centrifughe.

Nota a parte, questo sistema di propulsione unito al generatore di energia k 64, permetterà agli uomini di spostarsi nel sistema solare ed oltre, senza problemi di rifornimento di energia.

Non so come mi sia venuto in mente l’idea del sistema di propulsione inerziale, forse è stato la somma di molti particolari che ad un certo punto hanno completato lo schema

Foto N°1

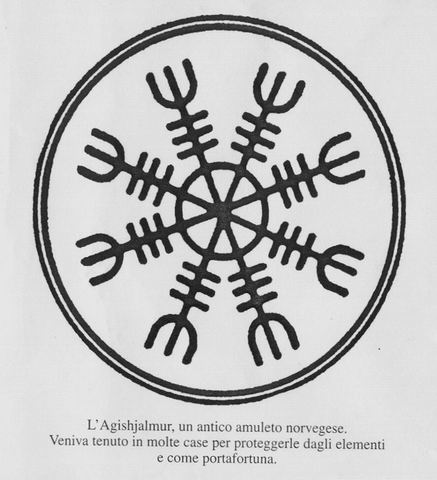
di sicuro ha contribuito molto il fatto di aver visto il disegno di questo amuleto Norvegese chiamato Agishjalmur.

Quando l’ho visto, mi ha subito colpito perchè mi ha fatto pensare ad un disegno meccanico in sezione.

In particolare sono state le tre lineette, poste al di sotto di quella specie di forca a tre denti che mi hanno illuminato.

Ho pensato che quelle volessero indicare una bobina elettromagnetica che può attirare, se attivata, la parte esterna, facendogli cambiare la posizione sulla circonferenza.

In questo modo, si può agire sulla variazione del raggio delle masse rispetto al centro, ottenendo così una “Curvatura” che determinerà una variazione delle forze centrifughe generate, come spigherò meglio più avanti.

Foto N°2

Oltre all’amuleto ha contribuito molto osservare alcuni “Cerchi nel Grano” come quello

nella foto a Lato.

Si può notare una grande somiglianza con l’agishjalmur e mi ha fatto comprendere come

sia possibile ottenere la Propulsione Inerziale.

Come potrete vedere il modello che ho ideato è molto simile a questo cerchio nel grano.

L’unica differenza tra il disegno del cerchio e il mio modello è che nel cerchio suggeriscono

un sistema elettromagnetico per ottenere la curvatura che darà lo sbilanciamento delle

forze, mentre io uso un sistema completamente meccanico.

I disegni che seguono, illustrano uno dei vari sistemi che si possono realizzare per ottenere una propulsione inerziale.

Foto N°3

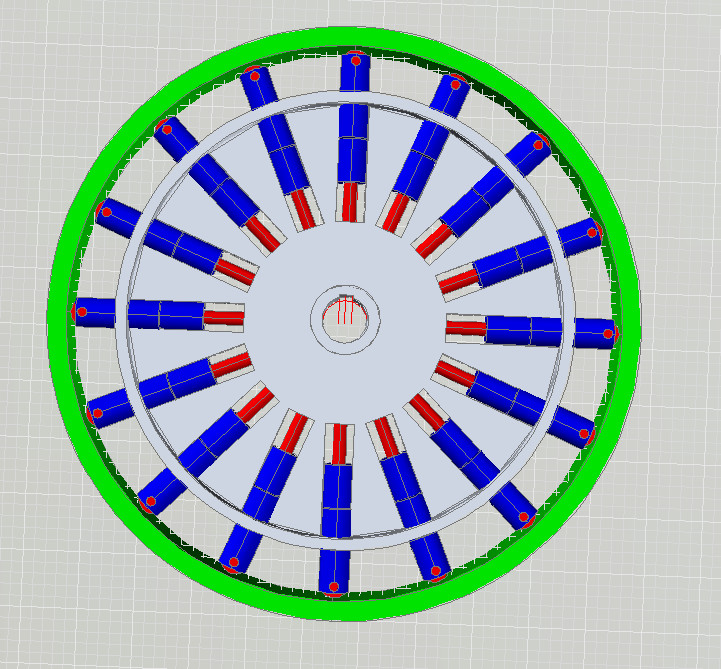
In questo modello tridimensionale, non ho messo il motore, per semplificare il tutto.

Le masse e tutto il sistema è perfettamente bilanciato perchè i raggi delle rispettive masse sono uguali e non c’è nessuna spinta in nessuna direzione.

Il sistema è molto semplice è composto da una parte che porta e fa ruotare le masse. I bulloni rossi, servono per impedire che le masse si allontanino

dal centro di rotazione quando si opererà con la variazione dei raggi delle masse stesse.

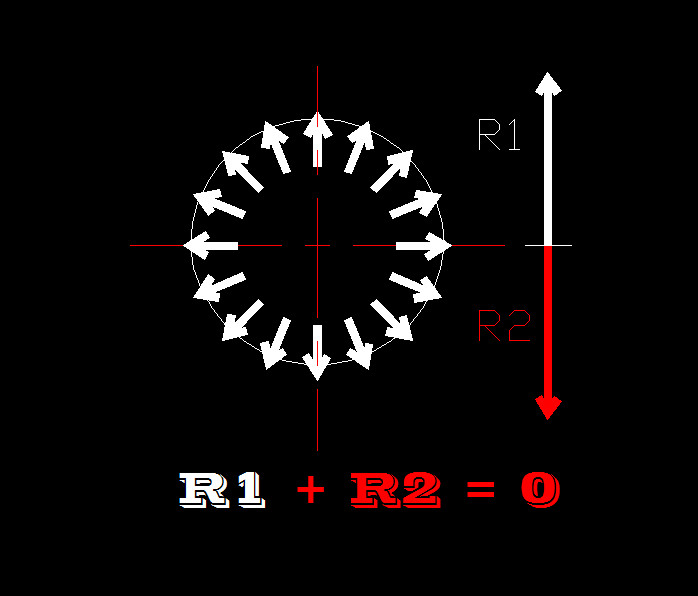
Il disegno soprastante è una rappresentazione delle forze centrifughe che si verranno a creare quando il sistema, nella posizione della Foto N°3 è in rotazione.

Come si può ben comprendere, quando il sistema è bilanciato tutte le forze sono uguali.

Ne consegue che la risultante delle forze della semicirconferenza superiore (R1 colorata di bianco) saranno uguali alla risultante delleforze della semicirconferenza inferiore ( R2 colorata in rosso), la somma delle due risultanti sarà quindi uguale a Zero

Le masse scorrevoli, sono il pezzo colorato in blu.

Foto N°4

Le parti in rosso sono un perno ed un cuscinetto. La massa è forata con un diametro maggiore pari al diametro della testa del bullone che le tratterrà, ed un ulteriore foro inferiore pari al diametro dello stelo del bullone.

Quì sotto possiamo vedere meglio alcuni particolari del disco per la rotazione delle masse.

Foto N°5

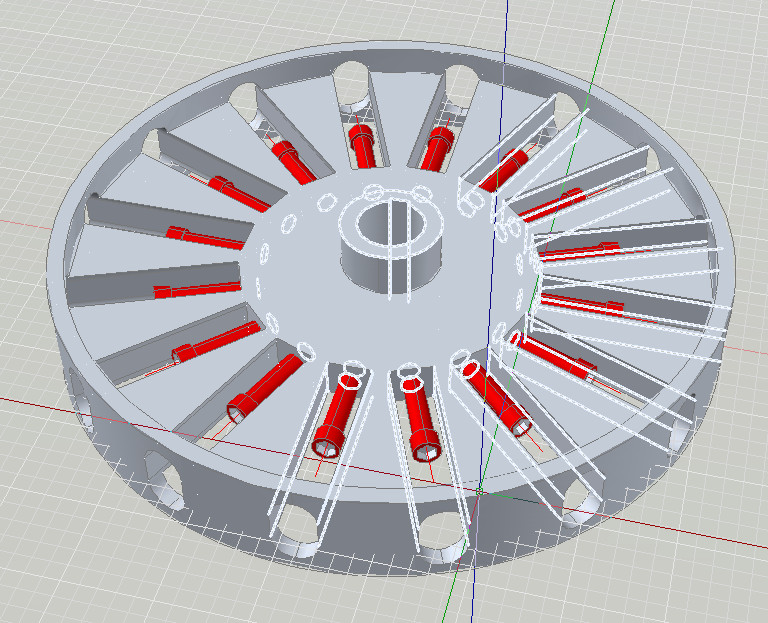
I fori ovali servono per impedire la rotazione su se stesse delle masse in modo da avere un corretto funzionamento del cuscinetto di rotolamento

sul cerchio verde quando ci sarà la “curvatura”.

Quanto segue è una dimostrazione fatta da un Astrofisico, Michele Moroni, che ho conosciuto personalmente e che ha gentilmente elaborato una

dimostrazione scientifica alla mia idea della propulsione Inerziale.

Il percorso su cui Lui ha fatto le sue analisi è diverso da quello reale, da una dimostrazione che il “sistema” avrà dei movimenti

oscillatori che al termine di una rotazione completa della massa il baricentro ritornerà nella sua posizione iniziale perchè nel

tratto iniziale che va da A ad B, non avendo variazioni sull’asse delle x, annullerà lo spostamento dovuto all’azione della Forza

centrifuga nel tratto semicircolare.

Ecco quindi la Sua dimostrazione.

Consideriamo una massa m che si muove vincolata alla traiettoria disegnata in figura sottostante

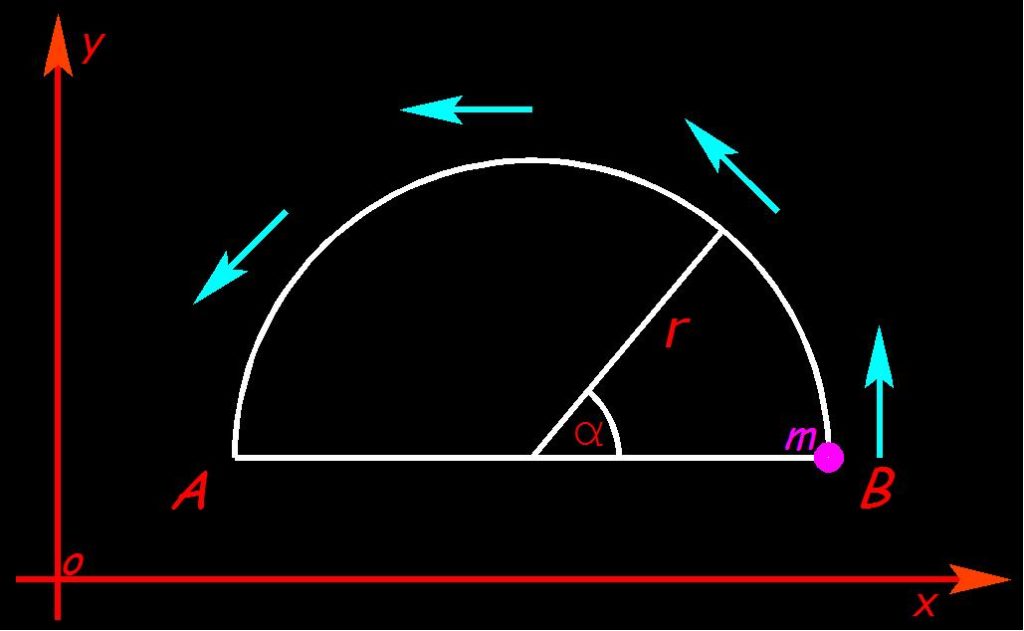
La traiettoria si trova al’ interno di un “Disco Volante” di massa M.

Risulta evidente che, durante l’intervallo di tempo in cui la massa m si trova nella semicirconferenza superiore

(Muovendosi da B ad A), questa esercita sul disco una forza centrifuga data da:

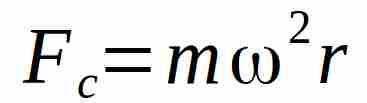
Il teorema dell’impulso afferma che la forza applicata ad un corpo per l’ intervallo su cui essa agisce è uguale alla cariazione della quantità di moto del corpo stesso.

Conseguentemente la componente di una forza applicata al disco lungo una determinata direzione moltiplicata per l’intervallo di tempo su cui essa agisce è uguale alla variazione della quantità di moto del disco in quella direzione.

La componente della forza lungo l’ asse delle x (vedi figura) è:

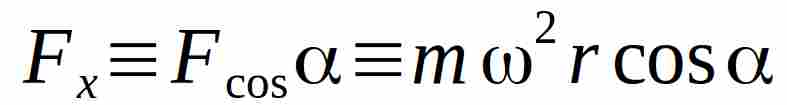
in virtù del teorema dell ‘impulso risulta quindi che nell’intervallo di tempo infinitesimo dt la variazione della quantità di moto del disco lungo la direzione y è:

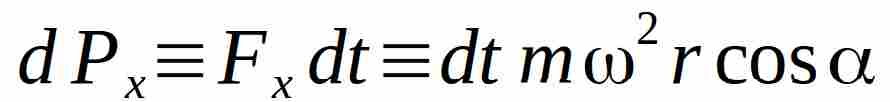
Sappiamo ora che l’ angolo alfa è legato al tempo t dalla relazione:

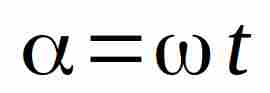
Quindi la precedente relazione può essere riscritta come

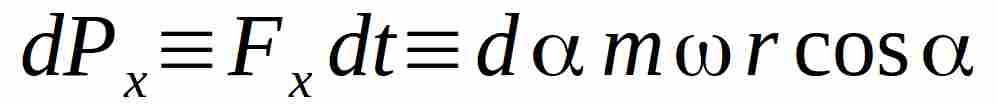
L’impulso acquistato dal disco durante il movimento della massa m sulla semicirconferenza è quindi:

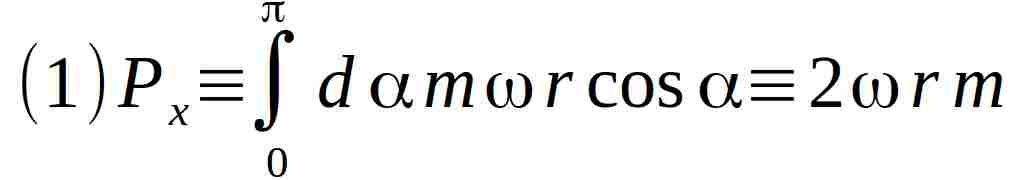
Durante il movimento sul segmento inferiore ovviamente non agisce alcuna forza .

Notiamo però che quando la massa m giunge al punto A è dotata di una quantità di moto lungo la direzione delle x data da:

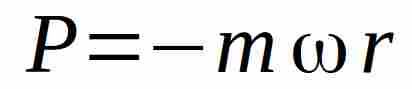
Durante il percorso tra A e B la quantità di moto Lungo X è Zero, mentre durante il passaggio al punto B, si riporta:

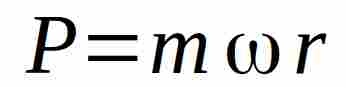
Resta quindi ovvio che la massa m durante il passaggio da A a B ha modificato la sua quantità di moto di un :

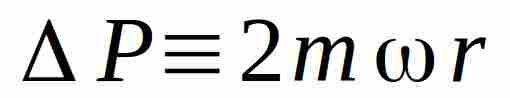
Durante il cambiamento di traiettoria ha quindi agito una forza vincolare tale da produrre questa variazione della quantità di moto.

Conseguentemente, per azione e reazione durante i cambiamenti di traiettoria agisce una forza di reazione tale da produrre un cambiamento della quantità di moto del disco:

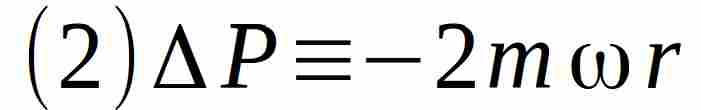
La variazione della quantità di moto totale del disco, quando la massa m fa un giro completo, è quindi data da

( 1 ) + ( 2 ) = 0

Resta quindi dimostrato che la reazione vincolare produce una forza che agisce sul moto del disco esattamente uguale alla forza centrifuga ma, in direzione opposta.

Quindi il disco, oscillerà attorno al suo baricentro, il quale è immobile nello spazio.

La dimostrazione dell’ oscillazione, generata dal percorso in figura, diventa quindi la prova scientifica della propulsione inerziale, in quanto il percorso reale è quello del disegno sottostante che è composto da due semicirconferenze dove la semicirconferenza che sostituisce il tratto rettilineo ha il centro di rotazione diverso come si può vedere nel disegno sottostante dove il percorso rettilineo da A ad B è stato sostituito con un percorso semicircolare con raggio variabile

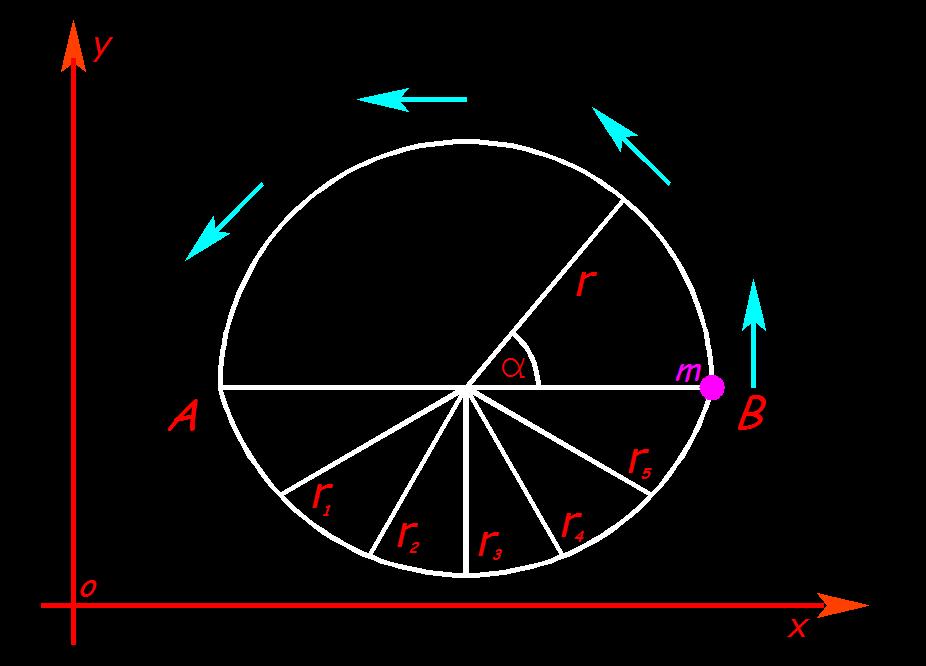
Questo particolare, oltre al fatto che non vi è una sola massa posta in rotazione, creerà una Forza centrifuga di valore diverso tra le due sezioni con direzione opposta.

La risultante di Tutte le Forze che agiscono darà lo spostamento desiderato.

Ed ecco finalmente il sistema di propulsione inerziale che sfrutta la Forza Centrifuga nella sua configurazione che permetterà di avere una spinta secondo una direzione voluta, in questo caso, Verso l’ alto.

Nella foto sottostante è illustrato il percorso reale che le masse saranno costrette a fare quando il disco esterno (verde) viene spostato verso l’alto.

Foto N°6

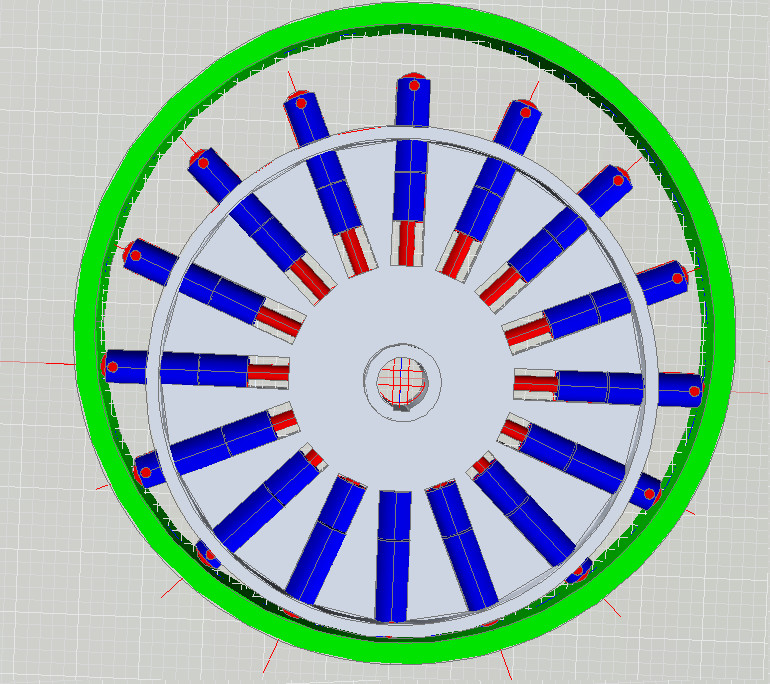
Vediamo chiaramente che le masse nella semicirconferenza inferiore, sono state avvicinate al centro per mezzo del cerchio verde.

In questo modo otteniamo delle forze centrifughe di valore diverso dalle loro antagoniste nella semicirconferenza superiore.

Nella semicirconferenza superiore, vediamo che le masse, non sfuggono per la tangente perchè, come ho spiegato prima, sono trattenute dalla testa del bullone rosso ed il loro raggio sarà sempre uguale al raggio massimo del meccanismo.

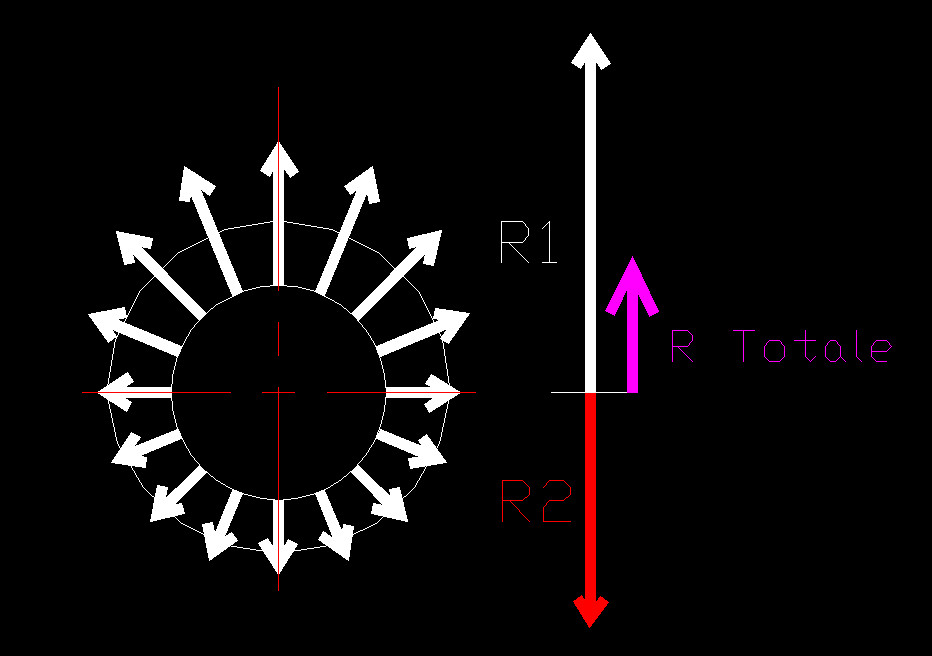
Nello schema soprastante vediamo l’ effetto della “curvatura” direzionale imposta alle masse.

Sappiamo che la formula della Forza centrifuga, in funzione del numero di giri è indicata dalla formula :

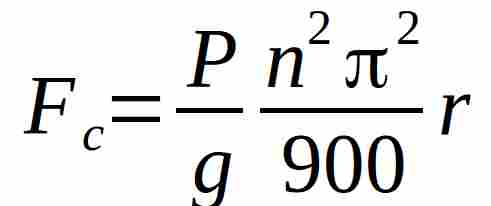
Considerando che Pi Greco al quadrato è quasi uguale al valore di g possiamo semplificarela formula della Forza Centrifuca in:

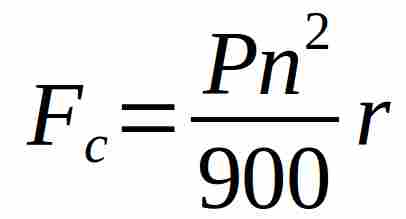
Dove:

P = Peso della massa,

n = Numero di giri al minuto,

g = 9,81

r = raggio e distanza dal centro di rotazione,

Si dovrebbe ora comprendere perfettamente, per il fatto che nella formula, essendo il raggio r un “moltiplicatore” dei valori , si ottengano dei valori maggiori nella semicirconferenza superiore, rispetto a quelli della semicirconferenza inferiore, dove il raggio r viene ridotto dal cerchio di contenimento

Facendo la risultante del “sistema di Forze” si otterrà così una forza, chiamata Risultante Totale, con direzione controllabile e variabile a piacere.

Nel momento in cui il valore della risultante, rivolta verso l’alto, supererà il peso del sistema, si otterrà l’annullamento localizzato della forza di gravità ed il sistema, si distaccherà dal suolo.

In ogni caso questo sistema, se usato al di fuori del campo gravitazionale terrestre, potrà spostare grandi masse con un piccolo sforzo.

Ecco dimostrato il sistema di propulsione usato dai dischi volanti.

L’unione di questo sistema di propulsione con il generatore che ho chiamato “Generatore K64” permetterà all’Uomo di viaggiare nell’universo senza bisogno di rifornimento di energia.

Per i viaggi tramite “tunnel spaziali” l’umanità, non è ancora pronta e quindi si deve, almeno per il momento, rimanere entro il sistema solare.